Data Placement

Every Hermes system instance includes one or more Hermes nodes.

A destination is a buffering resource that can be identified by a pair of node + target "coordinates."

Each target $t_k$ has characteristics such as the following:

• A capacity $Cap[t_k]$
• A remaining capacity $Rem[t_k]$
• A speed (or throughput) $Speed[...,t_k]$
  • This is the mean of the throughputs of all ranks associated with the destination's node.
  • Fix this! Speed is really a function of the origin.

Note: At any point in time, there's a degree of uncertainty to some of the destination characteristics. For example, the remaining capacity of a destination is typically obtained from a global metadata (MD) structure that is updated asynchronously. Only the Hermes node buffer pool managers have the precise value(s) for the pool under their management.

The Data Placement Problem

Given N storage targets, a data placement policy P, a cost function F, and a BLOB, a data placement consists of a BLOB partitioning and an assignment of those parts to storage targets that satisfies the constraints of the data placement policy and that minimizes the cost function.

• Epoch - interval within which we update targets (status).
  • Static (e.g., time interval or number of operations)
  • Dynamic, i.e., computed by the delta of status

[optional] Placement window - interval within which we make data placement decisions.

• Timer expired or I/O operation count reached, which ever comes first.
• Static (e.g., time interval or number of operations)
• Dynamic, i.e., number of put operations

Epoch and placement window could be aligned (static mode).

The data placement is done within Data Placement Engine (DPE) component in HERMES.

The Data Placement Loop

A placement schema $PS(b)$ of a BLOB $b (>0)$ is a decomposition $b = s_1+\cdots+s_k,\; s_i\in\mathbb{N}\setminus\{0\}$ together with a target mapping $(s_1,\ldots,s_k)\mapsto(t_1(s_1),\ldots,t_k(s_k))$.

A sequence of buffer IDs $(ID_1,\ldots,ID_A)$ conforms to a target assignment $(s, t)$, iff $s = \sum_{i=1}^A Size(ID_i)$ and $\forall i\;Target(ID_i) = t$.

An allocation of a placement schema is a sequence of buffer IDs which is the concatenation of conforming target assignments.

1. Given: a vector of BLOBs $(b_1, b_2,\ldots, b_B)$
2. The DPE creates placement schemas $PS(b_i),\;1\leq i\leq B$.
3. The placement schemas are presented to the buffer manager, which, for each placement schema, returns an allocation of that schema (or an error), and updates the underlying metadata structures.
4. I/O clients transfer data from the BLOBs to the buffers.

Problem to Solve in DPE

Input:

• Vector of BLOBs $(b_1, b_2,\ldots, b_B)$.
• Vector of targets $(t_1, t_2,\ldots, t_D)$.
• Vector of target remaining capacities $Rem[t_k], \;1\leq k\leq D$.
• Vector of target speed $Speed[t_k], \;1\leq k\leq D$.

Output:

• Placement schema $(s_1,\ldots,s_k)\mapsto(t_1(s_1),\ldots,t_k(s_k))$, where $b (>0)$ is a decomposition $b = s_1+\cdots+s_k,\; s_i\in\mathbb{N}\setminus\{0\}$

Data Placement Solution

1. Pick a DP solver to obtain a placement schema.
   • Linear programming
     • Constraints
     • Objective function
   • Round-robin
     • Granularity
   • Random
     • Distribution(s)
2. Use the buffer pool's "coin selector" to convert into buffer IDs.
3. Handle two types of potential errors.
   • DP solver failure: This can happen because of outdated target status, i.e., insufficient capacity, constraint infeasibility, etc.
     • Solution to insufficient capacity: epoch, decision windows, swap space.
     • Solution to constraint infeasibility: buffer reorganization, target filtering.
   • Coin selection failure: This can happen because of outdated state view information, e.g., outdated remaining capacities.
     • Solution: epoch, decision windows, swap space.

Error Handling

In both cases, the list of targets is inappropriate and needs to be updated or changed.

The list of "relevant destinations" for a rank is assembled by the Hermes node topology generator. It gets triggered when DP fails. The initial topology consists of "node-local" destinations (Plan A) plus a backup list of neighbors (Plan B) to consult when a rank gets in trouble. If both plans fail, the topology generator invokes the application-level "rebalancer" to redraw neighborhood boundaries (Plan C). In the past, we used to call these components node- and application-level DPEs, but they aren't directly involved in DP decisions, and we need maybe a clearer terminology.

Data Placement Solution Implementation

LP solver

• Pick Google OR-Tools as a linear optimization tool to obtain a placement schema.
  • Minimize client I/O time.

Round-robin solver

• Pick the next target if the remaining capacity is greater or equal to the BLOB size, otherwise check the one after the next target until a target with enough capacity is found.

Random solver

• Randomly pick a target from all targets which have the capacity greater or equal to the BLOB size.

Experimental Setup

Scaling the number of BLOBs, 10 GB total BLOB size

• Small size BLOBs: random within the range of 4KB to 64KB
• Medium size BLOBs: random within the range of 64KB to 1MB
• Large size BLOBs: random within the range of 1MB to 4MB
• Extra large size BLOBs: random with the range 4MB to 64MB
• Huge size BLOBs: fixed 1GB

Scaling the BLOB size, 1,000 and 8,192 BLOBs in total

• Fixed BLOB size of 4KB, 64KB, 1MB, 4MB, 64MB

Experimental Results

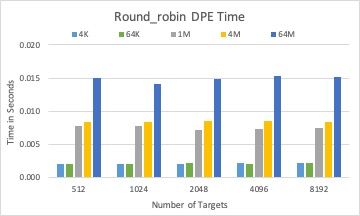
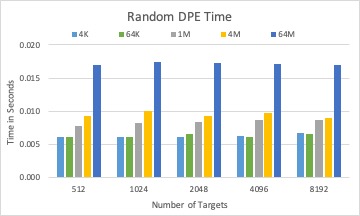
The DPE time of three different solvers with 10GB BLOBs in total.

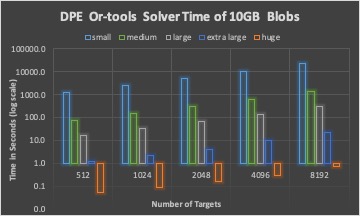
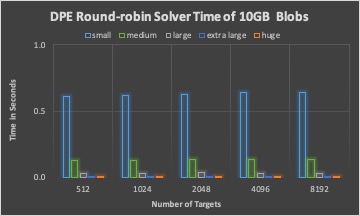
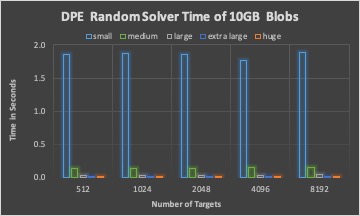
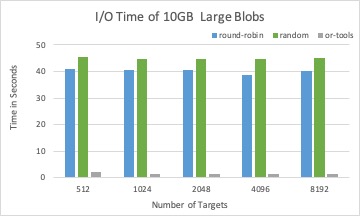
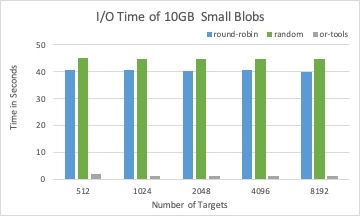
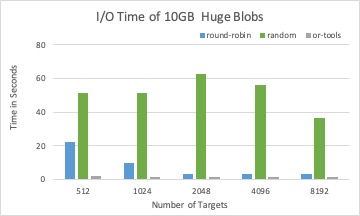
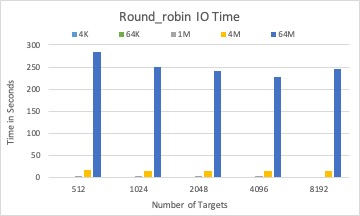
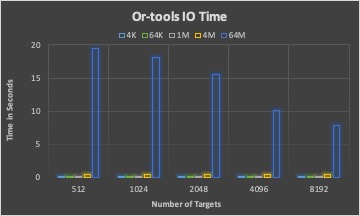
The associated I/O time of placement schema from three different solvers with 10GB BLOBs in total.

The DPE time of three different solvers with 1,000 BLOBs in total.

The associated I/O time by placement schema by three different solvers with 1,000 BLOBs in total.

Conclusions

For a fixed total size of many BLOBs, DPE time is increasing with the number of BLOBs for all solvers.

Round-robin and random solver can quickly calculate targets for a BLOB than LP solver, while not considering optimizing I/O time.

LP solver is efficient when the search space (number of targets) is not too large (for example, less than 1,024).

LP solver is a good candidate to place large size BLOBs, where the DPE time has less impact than the I/O time to the overall performance.

One of the possible policies is that size 64KB could be a boundary for BLOB aggregation. BLOB size less than 64KB will be aggregated within a placement window and than placed together to mitigate DPE impact.

Another possible policy is to use round-robin or random for small blobs and LP solver for large blobs.